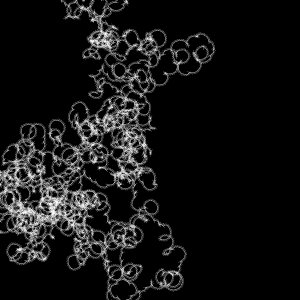
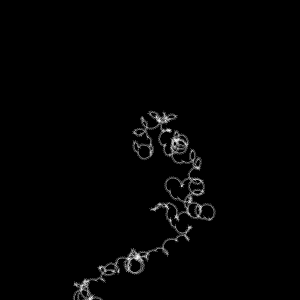
xn+1 = a xn (1 – xn) (0<a<4) で与えられるLogisticmapはコントロールパラメータaの値に応じて関数の振る舞いを変え、境界値a=3.5699456…でカオス的振る舞いをはじめる。
独自のシミュレーション方法で、Feigenbaum point周辺の振る舞いを可視化した。GCM-modelはLogisticmapをネットワークで繋いだカオス結合系モデル。
安定した構造のすぐ隣には不安定な構造が横たわっている。
どこまで安定領域を拡大しても、何度でも不安定な構造が現れるLogisticmapを別様のかたちで体験することができる。
安定と不安定の臨堺で、変動し、ぶれ続ける生成の機構がそこにはある。
Feigenbaum Point : around a=3.5699 (step=40000, scale=120)
Feigenbaum Point : around a=3.5699 (step=40000, scale=400)
Logistic Map : around a=3.63552 (step=50000, scale=5.0)
Logistic Map : around a=3.82841 (step=10000, scale=48)
GCM-Model: node30, a=1.8, e=0.12, odds=0.1 (step=4000, scale=20)
※これらのヴィジュアルデータは、僕の大学時代の研究の一部です。詳細はRESEARCHページの(Kazeto and Takashi, 2008)を御覧ください。
※These visual data is one of the outcomes of my research in undergraduate. Please check out more details on paper(Kazeto and Takashi, 2008) at RESEARCH page.